본 포스팅은 R for Data Science를 기반으로 하여 작성하였습니다.
1. 일반적인 값
막대 차트와 히스토그램 모두에서 긴 막대는 변수의 평범한 값을 표시하고 짧은 막대는 덜 일반적인(비정상적인) 값을 표시합니다. 막대가 없는 장소는 데이터에 표시되지 않은 값을 나타냅니다. 이 정보를 유용한 질문으로 바꾸려면 예상하지 못한 부분을 찾아내야 합니다.
- 어떤 값이 가장 일반적이고, 그 이유는 무엇일까?
- 어떤 값이 보기 드문 희귀한 값일까? 그 이유는 무엇일까? 내 생각과 일치하는가?
- 특이한 패턴이 보이나요? 특이 패턴을 설명할 수 있나?
예를 들어 아래 히스토그램은 몇 가지 흥미로운 질문을 제안합니다.
- 왜 전체 캐럿과 캐럿의 흔한 분수에 더 많은 다이아몬드가 있을까?
- 각 봉우리의 약간 왼쪽보다 각 봉우리의 약간 오른쪽에 더 많은 다이아몬드가 있는 이유는 무엇일까?
- 3캐럿보다 큰 다이아몬드는 왜 없을까?
ggplot(data = smaller, mapping = aes(x = carat)) +
____geom_histogram(binwidth = 0.01)

유사한 값의 군집은 데이터에 부분 군이 있음을 나타냅니다. 하위 그룹을 이해하려면 다음과 같은 추가 질문이 필요합니다.
- 각 군집 내의 관측값이 어떻게 서로 유사한가?
- 개별 군집의 관측값은 서로 어떻게 다른가요?
- 군집을 어떻게 설명할 수 있습니까?
- 클러스터의 모양이 오해의 소지가 있는 이유는 무엇일까?
아래의 히스토그램은 옐로스톤 국립공원에 있는 올드 페이스풀 간헐천의 272번의 분출 길이(분)를 보여줍니다. 분출 시간은 짧은 분출(약 2분)과 긴 분출(4~5분)의 두 그룹으로 분류되지만 그 사이 값은 거의 없습니다.
ggplot(data = faithful, mapping = aes(x = eruptions)) +
____geom_histogram(binwidth = 0.25)

위의 많은 질문은 예를 들어 한 변수의 값이 다른 변수의 동작을 설명할 수 있는지 확인하기 위해 변수 간의 관계를 탐색하라는 메시지를 내포하고 있습니다. 이어서 계속 변수 간의 관계를 파악해 보겠습니다.
2. 비정상적인 값
이상치는 비정상적인 관찰값(패턴에 맞지 않는 데이터 포인트)입니다. 때때로 이상치는 데이터 입력 오류인 경우가 있습니다. 다른 경우에는 이상치가 중요한 새로운 과학을 제안할 수도 있습니다. 데이터가 많은 경우에는 히스토그램에서 이상 값을 확인하기 어려운 경우가 있습니다. 예를 들어, diamonds 데이터 세트에서 y 변수의 분포를 가져옵니다. 이상 값의 유일한 증거는 x축의 비정상적으로 넓은 한계입니다.
ggplot(diamonds) +
____geom_histogram(mapping = aes(x = y), binwidth = 0.5)
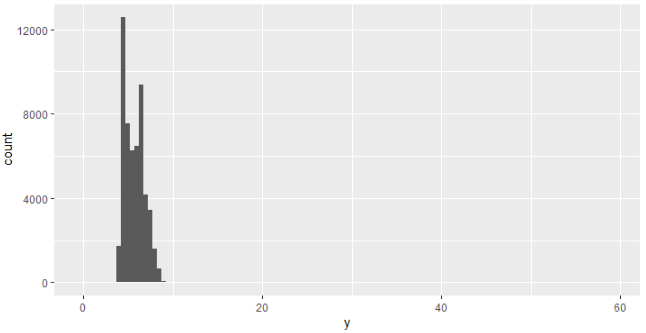
일반 구간 정의에는 관측값이 너무 많아서, 희귀 구간은 너무 짧아서 볼 수 없습니다. 비정상적인 값을 쉽게 볼 수 있도록 coord_cartesian()을 사용하여 y축을 확대하거나 축소해야 합니다.
ggplot(diamonds) +
____geom_histogram(mapping = aes(x = y), binwidth = 0.5) +
____coord_cartesian(ylim = c(0, 50))

(coord_cartesian()에는 x축을 확대해야 할 때를 위한 xlim() 인수도 있습니다. ggplot2에는 약간 다르게 작동하는 xlim() 및 ylim() 함수도 있습니다.)
이를 통해 0, ~30 및 ~60의 세 가지 비정상적인 값이 있음을 알 수 있습니다. 우리는 dplyr 패키지를 사용해서 비정상적인 값을 추출해 보겠습니다.
unusual <- diamonds %>%
____filter(y < 3 | y > 20) %>%
____select(price, x, y, z) %>%
____arrange(y)
unusual

y 변수는 이러한 다이아몬드의 세 가지 치수 중 하나를 mm 단위로 측정합니다. 우리는 다이아몬드의 너비가 0mm일 수 없다는 것을 알고 있으므로 이 값은 정확하지 않아야 합니다. 우리는 또한 32mm와 59mm의 측정이 타당하지 않다고 의심할 수도 있습니다. 이 다이아몬드는 길이가 1인치가 넘지만 수십만 달러가 필요하지는 않습니다.
이상치를 포함하거나 포함하지 않고 분석을 반복하는 것이 좋습니다. 결과에 미치는 영향이 미미하고 왜 존재하는지 알 수 없는 경우 결측값으로 대체하고 계속 진행하는 것이 합리적입니다. 그러나 결과에 상당한 영향을 미친다면 정당한 이유 없이 삭제해서는 안 됩니다. 원인(예: 데이터 입력 오류)을 파악하고 문서에서 해당 오류를 제거했음을 공개해야 합니다.
'R 프로그래밍 > R을 활용한 탐색적 자료 분석' 카테고리의 다른 글
| 탐색적 자료 분석(공변량2) (0) | 2021.09.30 |
|---|---|
| 탐색적 자료 분석(공변량1) (0) | 2021.09.29 |
| 탐색적 자료 분석(결측치 처리) (0) | 2021.09.28 |
| 탐색적 자료 분석(변수 분포 탐색) (0) | 2021.09.26 |
| 탐색적 자료 분석 Introduction (0) | 2021.09.25 |



댓글